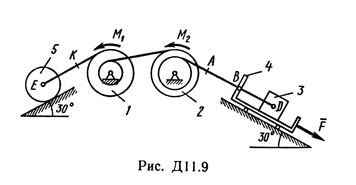
Решение Д11-95 (Рисунок Д11.9 условие 5 С.М Тарг 1989г)
Если общая сумма ваших покупок у продавца Михаил_Перович больше чем:
- 19510 ₽ скидка составит 15%
- 9755 ₽ скидка составит 10%
- 4877 ₽ скидка составит 7%
- 1951 ₽ скидка составит 5%
- 975 ₽ скидка составит 3%
- 488 ₽ скидка составит 2%
- 98 ₽ скидка составит 1%
Всего продано 1
Возвратов 0
Хороших отзывов 0
Плохих отзывов 0
Решение Д11-95 (Рисунок Д11.9 условие 5 С.М Тарг 1989г)
Механическая система состоит из тел 1, 2, …, 5 весом P1, Р2, …, P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R. На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, M2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована. Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты x, т. е. x = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты x см. «Указания»). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; для колес, обозначенных номером 4, Р4 — их общий вес (вес платформы такой тележки не учитывается).
Механическая система состоит из тел 1, 2, …, 5 весом P1, Р2, …, P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R. На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, M2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована. Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты x, т. е. x = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты x см. «Указания»). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; для колес, обозначенных номером 4, Р4 — их общий вес (вес платформы такой тележки не учитывается).