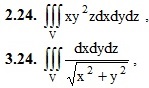ИДЗ 13.2 – Вариант 24. Решения Рябушко А.П.
Всего продано 4
Возвратов 0
Хороших отзывов 0
Плохих отзывов 0
1. Расставить пределы интегрирования в тройном интеграле если область V ограничена указанными поверхностями. Начертить область интегрирования
1.24. V: x ≥ 0, z ≥ 0, y = x, y = 3, z = 18 – x2 – y2
2. Вычислить данные тройные интегралы.
V: −2 ≤ x ≤ 1, 0 ≤ y ≤ 2, 0 ≤ z ≤ 3
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: x2 + y2 = 4y, y + z = 4, z ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.24. z ≥ 0, y = 2, y = x, z = x2
1.24. V: x ≥ 0, z ≥ 0, y = x, y = 3, z = 18 – x2 – y2
2. Вычислить данные тройные интегралы.
V: −2 ≤ x ≤ 1, 0 ≤ y ≤ 2, 0 ≤ z ≤ 3
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: x2 + y2 = 4y, y + z = 4, z ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.24. z ≥ 0, y = 2, y = x, z = x2
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате