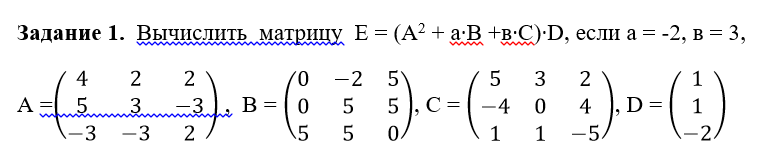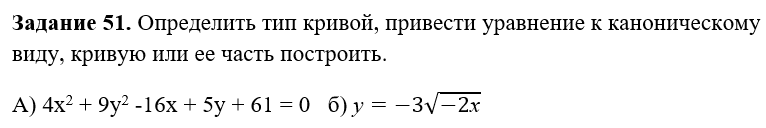ТГНГУ Эдукон Математика 1 семестр вариант 1
Всего продано 1
Возвратов 0
Хороших отзывов 0
Плохих отзывов 0
Задание 1. Вычислить матрицу Е = (А2 + а∙В +в∙С)∙D, если а = -2, в = 3,
Задание 11. Найти обратную для матрицы А, проверить, что А-1∙А = Е.
Задание 21. Найти решение системы линейных уравнений: а) по формулам Крамера и с помощью обратной матрицы; б) методом Гаусса.
Задание 31. Через точку М провести прямую параллельно, перпендикулярно и под углом 45 к прямой l. Сделать чертеж.
Задание 41. В треугольнике АВС известны координаты его вершин. Найти уравнение стороны АС, уравнение высоты, проведенной из вершины В, длину этой высоты, угол А.
А(0;8), В(-1;1), С(9;-4).
Задание 51. Определить тип кривой, привести уравнение к каноническому виду, кривую или ее часть построить.
А) 4х2 + 9у2 -16х + 5у + 61 = 0 б) у=-3√(-2х)
Задание 61. Убедиться, что векторы а,в, с не лежат в одной плоскости, написать разложение вектора х по векторам а, в, с.
x ⃗={15;-20;-1},a ⃗={0;2;1},b ⃗={0;1;-1},c ⃗={5;-3;2}
Задание 71. Точки А1, А2, А3, А4 являются вершинами пирамиды. Вычислить:
1) Длину ребра А1А2;
2) Угол между ребрами А1А2 и А3А2;
3) Площадь грани А1А2А3
4) объем пирамиды;
5) уравнение прямой А1А3;
6) Уравнение плоскости А2А3А4;
7) Уравнение высоты, опущенной из вершины А1 на грань А2А3А4;
8) длину этой высоты.
Сделать чертеж.
А1(1;-1;2), А2(2;1;2), А3(1;1;4), А4(6;-3;8).
Задание 81. Даны комплексные числа z1 и z2 в алгебраической форме. Записать их в тригонометрической и показательной форме и изобразить на комплексной плоскости. Выполнить действия: z1+z2, z1z2, z1:z2, z23. Найти все корни уравнения 3 –z1 =0, изобразить их на плоскости.
z1 =1 - √3 i, z2 = - i
Задание 11. Найти обратную для матрицы А, проверить, что А-1∙А = Е.
Задание 21. Найти решение системы линейных уравнений: а) по формулам Крамера и с помощью обратной матрицы; б) методом Гаусса.
Задание 31. Через точку М провести прямую параллельно, перпендикулярно и под углом 45 к прямой l. Сделать чертеж.
Задание 41. В треугольнике АВС известны координаты его вершин. Найти уравнение стороны АС, уравнение высоты, проведенной из вершины В, длину этой высоты, угол А.
А(0;8), В(-1;1), С(9;-4).
Задание 51. Определить тип кривой, привести уравнение к каноническому виду, кривую или ее часть построить.
А) 4х2 + 9у2 -16х + 5у + 61 = 0 б) у=-3√(-2х)
Задание 61. Убедиться, что векторы а,в, с не лежат в одной плоскости, написать разложение вектора х по векторам а, в, с.
x ⃗={15;-20;-1},a ⃗={0;2;1},b ⃗={0;1;-1},c ⃗={5;-3;2}
Задание 71. Точки А1, А2, А3, А4 являются вершинами пирамиды. Вычислить:
1) Длину ребра А1А2;
2) Угол между ребрами А1А2 и А3А2;
3) Площадь грани А1А2А3
4) объем пирамиды;
5) уравнение прямой А1А3;
6) Уравнение плоскости А2А3А4;
7) Уравнение высоты, опущенной из вершины А1 на грань А2А3А4;
8) длину этой высоты.
Сделать чертеж.
А1(1;-1;2), А2(2;1;2), А3(1;1;4), А4(6;-3;8).
Задание 81. Даны комплексные числа z1 и z2 в алгебраической форме. Записать их в тригонометрической и показательной форме и изобразить на комплексной плоскости. Выполнить действия: z1+z2, z1z2, z1:z2, z23. Найти все корни уравнения 3 –z1 =0, изобразить их на плоскости.
z1 =1 - √3 i, z2 = - i